DeepMind researchers have developed AlphaGeometry, an AI system with unprecedented ability to solve Olympiad-level geometry problems.
Olympiad math problems are complex mathematical problems typically posed in international mathematics competitions, such as the International Mathematical Olympiad (IMO).
These problems require a deep understanding of mathematical concepts, creative problem-solving skills, and rigorous logical reasoning, covering areas like algebra, combinatorics, and geometry, which this research targets.
The DeepMind study, published in Nature, marks a milestone advancement in AI’s problem-solving capabilities in mathematics.
The model system, dubbed AlphaGeometry, successfully solved 25 out of 30 problems from the International Mathematical Olympiad, a huge improvement over the previous state-of-the-art AI system, which solved only 10.
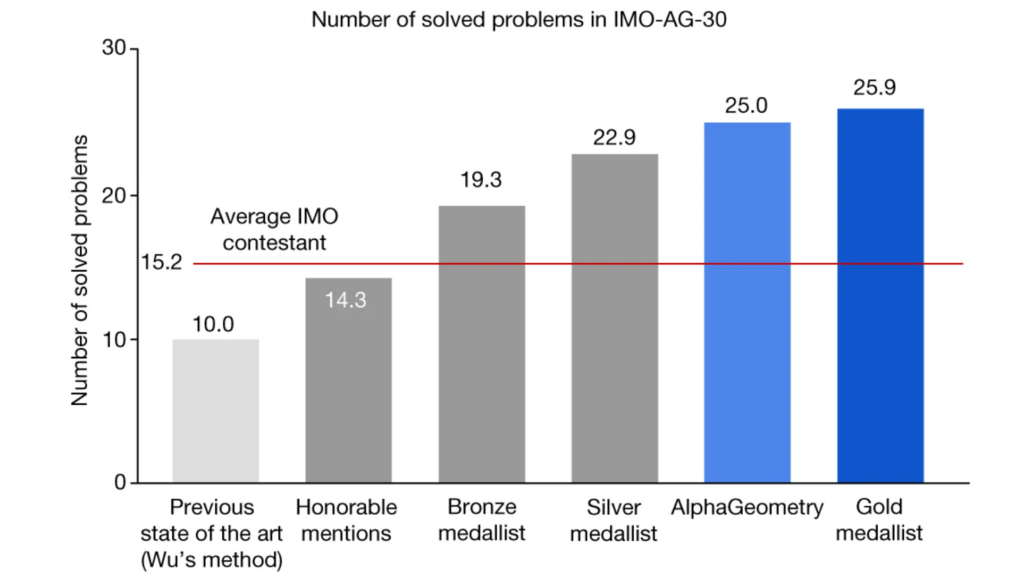
It nearly mirrors the performance of human gold medalists, who averaged solving 25.9 problems – which is a pretty remarkable nod to the skills of human Olympiads. Study author Trieu H. Trinh describes the paper below.
To achieve this, the AI system combines a neural language model with a symbolic deduction engine. The neural model rapidly suggests potential constructs, and the symbolic engine rigorously deduces solutions. This dual approach facilitates a balance between speed and accuracy in problem-solving.
A key to AlphaGeometry’s success is the generation of 100 million unique synthetic training examples. This approach allowed the AI to train without human input, overcoming a major data bottleneck.
Fields Medalist and IMO Gold Medalist Ngô Bảo Châu expressed his astonishment at this achievement, stating in a Google blog post, “It makes perfect sense to me now that researchers in AI are trying their hands on the IMO geometry problems first because finding solutions for them works a little bit like chess in the sense that we have a rather small number of sensible moves at every step. But I still find it stunning that they could make it work. It’s an impressive achievement.”
Evan Chen, a math coach, and former Olympiad gold medalist, also praised the AI: “AlphaGeometry’s output is impressive because it’s both verifiable and clean…It uses classical geometry rules with angles and similar triangles just as students do.”
Check out Chen’s video on the Olympiad below to get a sense of how outrageously hard these problems are.
AlphaGeometry’s capability to solve complex geometry problems at an Olympiad level not only demonstrates AI’s growing ability to reason logically but also opens new possibilities in mathematics and AI development.
It contributes to several breakthrough research from DeepMind, including GNoME, RT-2, AutoRT, FunSearch, AlphaMissense, and AlphaFold, to name but a few from recent memory.
More about the study
Here’s how AlphaGeometry works in five distilled steps:
- Synthetic theorem generation: AlphaGeometry starts by generating a massive set of random geometric problems. This is done by creating a variety of geometric statements, like “point A is on line segment BC” or “angle XYZ is 45 degrees.” These statements form the premises or starting points for potential theorems.
- Symbolic deduction: Using these premises, the AI’s symbolic deduction engine begins to reason out conclusions. It applies geometric rules and logic to derive new statements from the given premises, systematically exploring different combinations and relationships.
- Creating auxiliary constructions: Often, solving complex geometry problems requires introducing new elements (like additional points or lines) that aren’t part of the original setup. These are called auxiliary constructions. AlphaGeometry’s engine is designed to identify when and what auxiliary constructions are needed to progress toward a solution.
- Training the language model: A transformer-based language model is trained on the data generated from the above steps. This model learns to understand the patterns and logic in geometric reasoning. It gets better at predicting which auxiliary constructions or steps might be needed to solve similar problems in the future.
- Iterative problem solving: In the final step, AlphaGeometry tackles new geometry problems by combining the predictive power of its language model with the logical rigor of its symbolic deduction engine. The AI proposes auxiliary constructions and checks if they lead to a solution, iterating this process until it finds valid proof or exhausts its options.
DeepMind’s appetite for solving research problems in machine learning certainly has only grown, and this yet again illustrates AI’s pace of development. However, let’s not forget that human math Olympiads still have the edge – just.





