Les chercheurs de DeepMind ont mis au point AlphaGeometry, un système d'IA doté d'une capacité sans précédent à résoudre des problèmes de géométrie de niveau olympique.
Les problèmes mathématiques des Olympiades sont des problèmes mathématiques complexes généralement posés lors de concours internationaux de mathématiques, tels que les Olympiades internationales de mathématiques (OIM).
Ces problèmes nécessitent une compréhension approfondie des concepts mathématiques, des compétences créatives en matière de résolution de problèmes et un raisonnement logique rigoureux, couvrant des domaines tels que l'algèbre, la combinatoire et la géométrie, que cette recherche cible.
Les DeepMind étudepubliée dans la revue Nature, marque une avancée importante dans les capacités de résolution de problèmes mathématiques de l'IA.
Le système modèle, baptisé AlphaGeometry, a résolu avec succès 25 des 30 problèmes de l'Olympiade internationale de mathématiques, ce qui représente une amélioration considérable par rapport au système d'IA précédent, qui n'en avait résolu que 10.
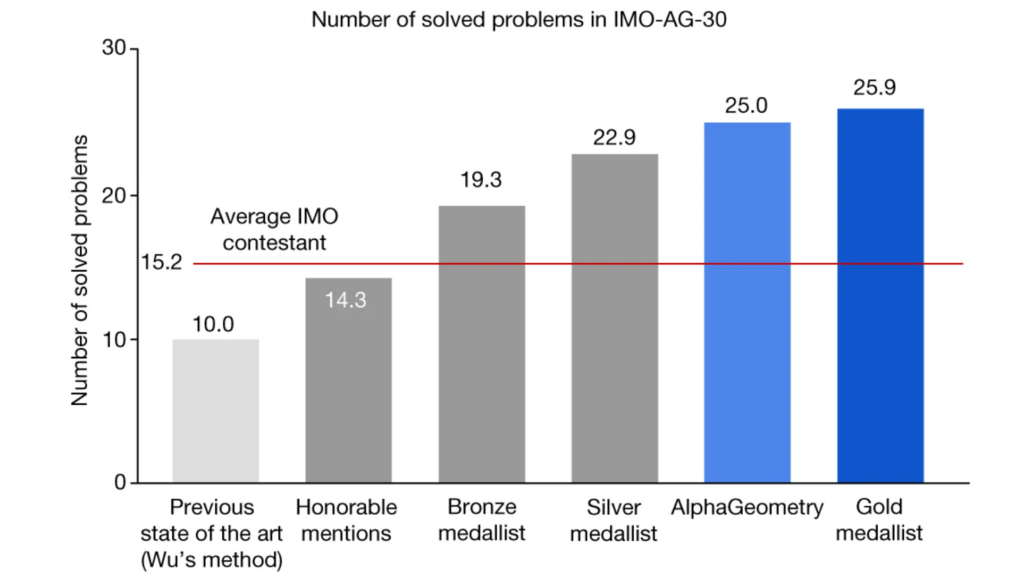
Cette performance est presque identique à celle des médaillés d'or humains, qui ont résolu en moyenne 25,9 problèmes, ce qui est un clin d'œil assez remarquable aux compétences des olympiades humaines. L'auteur de l'étude, Trieu H. Trinh, auteur de l'étude, décrit l'article ci-dessous.
Pour ce faire, le système d'IA combine un modèle de langage neuronal et un moteur de déduction symbolique. Le modèle neuronal suggère rapidement des constructions potentielles et le moteur symbolique déduit rigoureusement les solutions. Cette double approche permet de trouver un équilibre entre rapidité et précision dans la résolution des problèmes.
L'une des clés du succès d'AlphaGeometry est la génération de 100 millions d'exemples d'entraînement synthétiques uniques. Cette approche a permis à l'IA de s'entraîner sans intervention humaine, surmontant ainsi un important goulot d'étranglement au niveau des données.
Ngô Bảo Châu, médaillé Fields et médaillé d'or de l'OMI, a exprimé son étonnement face à cette réussite, dans un article du blog de GooglePour moi, il est tout à fait logique que les chercheurs en IA s'attaquent d'abord aux problèmes de géométrie de l'OMI, car la recherche de solutions fonctionne un peu comme aux échecs, en ce sens que nous disposons d'un nombre assez restreint de mouvements raisonnables à chaque étape. Mais je reste stupéfait de voir qu'ils ont réussi à faire fonctionner ce système. C'est une réussite impressionnante.
Evan Chen, coach en mathématiques et ancien médaillé d'or aux Olympiades, a également fait l'éloge de l'IA : "Les résultats d'AlphaGeometry sont impressionnants parce qu'ils sont à la fois vérifiables et propres... Elle utilise les règles classiques de la géométrie avec les angles et les triangles similaires, tout comme le font les étudiants.
Regardez la vidéo de Chen sur les Olympiades ci-dessous pour vous faire une idée de l'extrême difficulté de ces problèmes.
La capacité d'AlphaGeometry à résoudre des problèmes de géométrie complexes au niveau des Olympiades démontre non seulement la capacité croissante de l'IA à raisonner logiquement, mais ouvre également de nouvelles possibilités dans le domaine des mathématiques et du développement de l'IA.
Il contribue à plusieurs avancées de la recherche de DeepMind, notamment GNoME, RT-2, AutoRT, FunSearch, AlphaMissenseet AlphaFoldpour n'en citer que quelques-uns de mémoire récente.
En savoir plus sur l'étude
Voici comment AlphaGeometry fonctionne en cinq étapes distillées :
- Génération de théorèmes synthétiques: AlphaGeometry commence par générer un ensemble massif de problèmes géométriques aléatoires. Cela se fait en créant une variété d'énoncés géométriques, comme "le point A est sur le segment de droite BC" ou "l'angle XYZ est de 45 degrés". Ces énoncés constituent les prémisses ou les points de départ de théorèmes potentiels.
- Déduction symbolique: À partir de ces prémisses, le moteur de déduction symbolique de l'IA commence à raisonner en termes de conclusions. Il applique des règles géométriques et logiques pour dériver de nouvelles affirmations à partir des prémisses données, en explorant systématiquement différentes combinaisons et relations.
- Créer des constructions auxiliaires: Souvent, la résolution de problèmes géométriques complexes nécessite l'introduction de nouveaux éléments (comme des points ou des lignes supplémentaires) qui ne font pas partie de la configuration d'origine. Ces éléments sont appelés constructions auxiliaires. Le moteur d'AlphaGeometry est conçu pour identifier quand et quelles constructions auxiliaires sont nécessaires pour progresser vers une solution.
- Formation du modèle linguistique: Un modèle de langage basé sur un transformateur est formé sur les données générées par les étapes ci-dessus. Ce modèle apprend à comprendre les modèles et la logique du raisonnement géométrique. Il devient plus apte à prédire quelles constructions ou étapes auxiliaires pourraient être nécessaires pour résoudre des problèmes similaires à l'avenir.
- Résolution itérative de problèmes: Dans l'étape finale, AlphaGeometry aborde de nouveaux problèmes de géométrie en combinant le pouvoir prédictif de son modèle de langage avec la rigueur logique de son moteur de déduction symbolique. L'IA propose des constructions auxiliaires et vérifie si elles mènent à une solution, itérant ce processus jusqu'à ce qu'elle trouve une preuve valide ou qu'elle épuise ses options.
L'appétit de DeepMind pour la résolution de problèmes de recherche dans le domaine de l'apprentissage automatique n'a fait que croître, ce qui illustre une fois de plus le rythme de développement de l'IA. Toutefois, n'oublions pas que les Olympiades de mathématiques humaines ont toujours l'avantage - de justesse.





