DeepMind-Forscher haben AlphaGeometry entwickelt, ein KI-System mit einer beispiellosen Fähigkeit, Geometrieaufgaben auf Olympia-Niveau zu lösen.
Mathematik-Olympiade-Probleme sind komplexe mathematische Probleme, die typischerweise in internationalen Mathematikwettbewerben gestellt werden, wie z. B. der Internationalen Mathematik-Olympiade (IMO).
Diese Probleme erfordern ein tiefes Verständnis mathematischer Konzepte, kreative Problemlösungsfähigkeiten und strenges logisches Denken, das Bereiche wie Algebra, Kombinatorik und Geometrie abdeckt, auf die diese Forschung abzielt.
Die DeepMind StudieDie in der Fachzeitschrift Nature veröffentlichte Studie ist ein Meilenstein in der Entwicklung der Problemlösungskompetenz von KI in der Mathematik.
Das Modellsystem mit dem Namen AlphaGeometry hat 25 von 30 Aufgaben der Internationalen Mathematik-Olympiade erfolgreich gelöst, was eine enorme Verbesserung gegenüber dem bisherigen KI-System darstellt, das nur 10 Aufgaben lösen konnte.
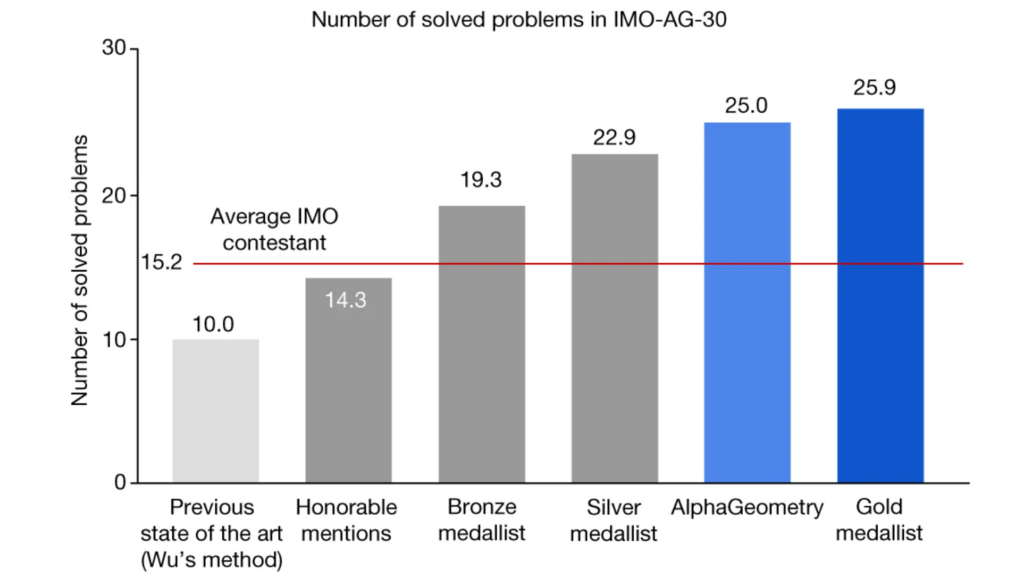
Dies entspricht fast der Leistung der menschlichen Goldmedaillengewinner, die im Durchschnitt 25,9 Probleme lösten - ein bemerkenswerter Vergleich mit den Fähigkeiten der menschlichen Olympioniken. Studienautor Trieu H. Trinh beschreibt die Arbeit im Folgenden.
Um dies zu erreichen, kombiniert das KI-System ein neuronales Sprachmodell mit einer symbolischen Deduktionsmaschine. Das neuronale Modell schlägt schnell potenzielle Konstruktionen vor, und das symbolische System leitet die Lösungen rigoros ab. Dieser duale Ansatz ermöglicht ein Gleichgewicht zwischen Geschwindigkeit und Genauigkeit bei der Problemlösung.
Ein Schlüssel zum Erfolg von AlphaGeometry ist die Generierung von 100 Millionen einzigartigen synthetischen Trainingsbeispielen. Dieser Ansatz ermöglichte es der KI, ohne menschliche Eingaben zu trainieren und so einen großen Datenengpass zu überwinden.
Der Fields-Medaillengewinner und IMO-Goldmedaillengewinner Ngô Bảo Châu äußerte sein Erstaunen über diese Leistung, in einem Google-Blogpost erklärtFür mich macht es jetzt absolut Sinn, dass die KI-Forscher sich zuerst an den IMO-Geometrieproblemen versuchen, denn die Lösung dieser Probleme funktioniert ein wenig wie beim Schach, da wir bei jedem Schritt eine relativ kleine Anzahl sinnvoller Züge haben. Aber ich finde es trotzdem erstaunlich, dass sie es geschafft haben. Das ist eine beeindruckende Leistung."
Evan Chen, ein Mathe-Coach und ehemaliger Goldmedaillengewinner der Olympiade, lobte die KI ebenfalls: "Die Ergebnisse von AlphaGeometry sind beeindruckend, weil sie sowohl überprüfbar als auch sauber sind... Es verwendet klassische Geometrie-Regeln mit Winkeln und ähnlichen Dreiecken, genau wie es Schüler tun."
Schauen Sie sich Chens Video über die Olympiade an, um ein Gefühl dafür zu bekommen, wie unverschämt schwer diese Probleme sind.
Die Fähigkeit von AlphaGeometry, komplexe Geometrieprobleme auf Olympia-Niveau zu lösen, demonstriert nicht nur die wachsende Fähigkeit der KI, logisch zu denken, sondern eröffnet auch neue Möglichkeiten in der Mathematik und der KI-Entwicklung.
Es trägt zu mehreren bahnbrechenden Forschungsergebnissen von DeepMind bei, darunter GNoME, RT-2, AutoRT, FunSearch, AlphaMissenseund AlphaFold, um nur einige aus der jüngsten Vergangenheit zu nennen.
Mehr über die Studie
Hier ist, wie AlphaGeometry in fünf Schritten funktioniert:
- Synthetische Theoriegenerierung: AlphaGeometry beginnt mit der Generierung einer großen Anzahl von zufälligen geometrischen Problemen. Dies geschieht durch die Erstellung einer Vielzahl von geometrischen Aussagen, wie "Punkt A liegt auf dem Liniensegment BC" oder "Winkel XYZ ist 45 Grad". Diese Aussagen bilden die Prämissen oder Ausgangspunkte für mögliche Theoreme.
- Symbolische Deduktion: Ausgehend von diesen Prämissen beginnt die symbolische Deduktionsmaschine der KI, Schlussfolgerungen zu ziehen. Sie wendet geometrische Regeln und Logik an, um neue Aussagen aus den gegebenen Prämissen abzuleiten, wobei sie systematisch verschiedene Kombinationen und Beziehungen untersucht.
- Erstellen von Hilfskonstruktionen: Die Lösung komplexer geometrischer Probleme erfordert oft die Einführung neuer Elemente (wie zusätzliche Punkte oder Linien), die nicht Teil des ursprünglichen Aufbaus sind. Diese werden Hilfskonstruktionen genannt. Die AlphaGeometry-Engine ist so konzipiert, dass sie erkennt, wann und welche Hilfskonstruktionen erforderlich sind, um eine Lösung zu finden.
- Training des Sprachmodells: Ein transformatorbasiertes Sprachmodell wird auf den Daten trainiert, die in den oben genannten Schritten erzeugt wurden. Dieses Modell lernt, die Muster und die Logik in der geometrischen Argumentation zu verstehen. Es kann immer besser vorhersagen, welche Hilfskonstruktionen oder -schritte in Zukunft zur Lösung ähnlicher Probleme benötigt werden.
- Iterative Problemlösung: Im letzten Schritt geht AlphaGeometry neue Geometrieprobleme an, indem es die Vorhersagekraft seines Sprachmodells mit der logischen Strenge seiner symbolischen Deduktionsmaschine kombiniert. Die KI schlägt Hilfskonstruktionen vor und prüft, ob sie zu einer Lösung führen. Dieser Prozess wird so lange wiederholt, bis ein gültiger Beweis gefunden oder die Möglichkeiten ausgeschöpft sind.
Der Appetit von DeepMind auf die Lösung von Forschungsproblemen im Bereich des maschinellen Lernens ist zweifellos nur gewachsen, was einmal mehr das Entwicklungstempo der KI verdeutlicht. Vergessen wir aber nicht, dass menschliche Mathematik-Olympiaden immer noch im Vorteil sind - knapp.





