Los investigadores de DeepMind han desarrollado AlphaGeometry, un sistema de IA con una capacidad sin precedentes para resolver problemas de geometría de nivel olímpico.
Los problemas matemáticos de olimpiada son problemas matemáticos complejos que suelen plantearse en competiciones internacionales de matemáticas, como la Olimpiada Matemática Internacional (OMI).
Estos problemas requieren una profunda comprensión de los conceptos matemáticos, capacidad creativa para resolver problemas y un razonamiento lógico riguroso, que abarque áreas como el álgebra, la combinatoria y la geometría, a las que se dirige esta investigación.
En DeepMind estudiarpublicado en Nature, marca un hito en la capacidad de la IA para resolver problemas matemáticos.
El sistema modelo, bautizado como AlphaGeometry, resolvió con éxito 25 de los 30 problemas de la Olimpiada Matemática Internacional, lo que supone una enorme mejora con respecto al anterior sistema de IA de última generación, que sólo resolvió 10.
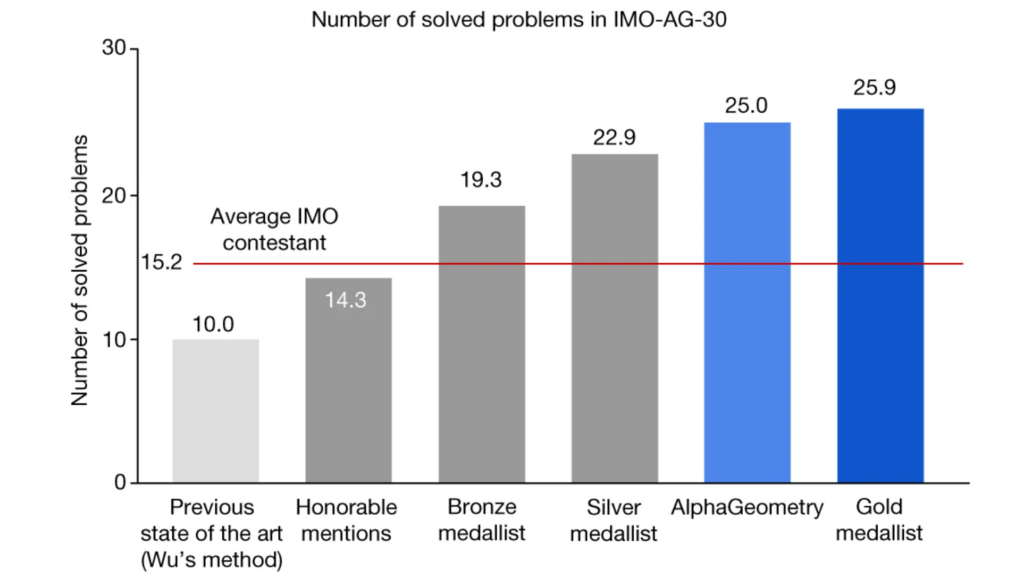
Casi refleja el rendimiento de los medallistas de oro humanos, que resolvieron una media de 25,9 problemas, lo que supone un guiño bastante notable a las habilidades de los olímpicos humanos. El autor del estudio, Trieu H. Trinh describe el trabajo a continuación.
Para lograrlo, el sistema de IA combina un modelo de lenguaje neuronal con un motor de deducción simbólica. El modelo neuronal sugiere rápidamente posibles construcciones, y el motor simbólico deduce rigurosamente las soluciones. Este doble enfoque facilita un equilibrio entre velocidad y precisión en la resolución de problemas.
Una de las claves del éxito de AlphaGeometry es la generación de 100 millones de ejemplos de entrenamiento sintéticos únicos. Este enfoque permitió a la IA entrenarse sin intervención humana, superando un importante cuello de botella de datos.
El medallista Fields y medalla de oro de la OMI Ngô Bảo Châu expresó su asombro ante este logro, en una entrada del blog de GooglePara mí tiene mucho sentido que los investigadores en Inteligencia Artificial se dediquen primero a los problemas de geometría de la OMI, porque encontrar soluciones se parece un poco al ajedrez, en el sentido de que tenemos un número bastante reducido de movimientos sensatos en cada paso. Pero me sigue pareciendo asombroso que hayan podido hacerlo funcionar. Es un logro impresionante".
Evan Chen, entrenador de matemáticas y antiguo medallista de oro en las Olimpiadas, también elogió la IA: "Los resultados de AlphaGeometry son impresionantes porque son verificables y limpios... Utiliza las reglas clásicas de la geometría con ángulos y triángulos semejantes, igual que hacen los estudiantes".
Echa un vistazo al vídeo de Chen sobre la Olimpiada para hacerte una idea de lo escandalosamente difíciles que son estos problemas.
La capacidad de AlphaGeometry para resolver complejos problemas de geometría a nivel olímpico no sólo demuestra la creciente capacidad de razonamiento lógico de la IA, sino que también abre nuevas posibilidades en el desarrollo de las matemáticas y la IA.
Contribuye a varias investigaciones revolucionarias de DeepMind, entre ellas GNoME, RT-2, AutoRT, FunSearch, AlphaMissensey AlphaFoldpor nombrar sólo algunos de los más recientes.
Más información sobre el estudio
He aquí cómo funciona AlphaGeometry en cinco pasos destilados:
- Generación de teoremas sintéticos: AlphaGeometry comienza generando un conjunto masivo de problemas geométricos aleatorios. Esto se hace mediante la creación de una variedad de enunciados geométricos, como "el punto A está en el segmento de línea BC" o "el ángulo XYZ es de 45 grados". Estos enunciados forman las premisas o puntos de partida de teoremas potenciales.
- Deducción simbólica: A partir de estas premisas, el motor de deducción simbólica de la IA empieza a razonar las conclusiones. Aplica reglas geométricas y lógicas para deducir nuevas afirmaciones a partir de las premisas dadas, explorando sistemáticamente distintas combinaciones y relaciones.
- Crear construcciones auxiliares: A menudo, para resolver problemas geométricos complejos es necesario introducir nuevos elementos (como puntos o líneas adicionales) que no forman parte de la configuración original. Estos elementos se denominan construcciones auxiliares. El motor de AlphaGeometry está diseñado para identificar cuándo y qué construcciones auxiliares son necesarias para avanzar hacia una solución.
- Entrenamiento del modelo lingüístico: Se entrena un modelo de lenguaje basado en transformadores a partir de los datos generados en los pasos anteriores. Este modelo aprende a comprender los patrones y la lógica del razonamiento geométrico. Mejora en la predicción de qué construcciones auxiliares o pasos podrían ser necesarios para resolver problemas similares en el futuro.
- Resolución iterativa de problemas: En el último paso, AlphaGeometry aborda nuevos problemas de geometría combinando el poder predictivo de su modelo lingüístico con el rigor lógico de su motor de deducción simbólica. La IA propone construcciones auxiliares y comprueba si conducen a una solución, iterando este proceso hasta que encuentra una prueba válida o agota sus opciones.
El apetito de DeepMind por resolver problemas de investigación en aprendizaje automático no ha hecho más que crecer, lo que ilustra una vez más el ritmo de desarrollo de la IA. Sin embargo, no hay que olvidar que las olimpiadas matemáticas humanas siguen teniendo ventaja... por poco.





